define even and odd function|odd or even function : Clark Even and Odd. The only function that is even and odd is f(x) = 0. Special Properties. Adding: The sum of two even functions is even; The sum of two odd functions is odd; The sum of an even and odd function is neither even nor odd (unless one function is zero). Multiplying: The product of two . Tingnan ang higit pa Watch Viral / Trending XXX porn videos. These are the best clips from the Philippines.
define even and odd function,Even and Odd. The only function that is even and odd is f(x) = 0. Special Properties. Adding: The sum of two even functions is even; The sum of two odd functions is odd; The sum of an even and odd function is neither even nor odd (unless one function is zero). Multiplying: The product of two . Tingnan ang higit paA function is "even" when: f(x) = f(−x) for all x In other words there is symmetry about the y-axis(like a reflection): This is the curve f(x) = x2+1 They got called "even" . Tingnan ang higit pa

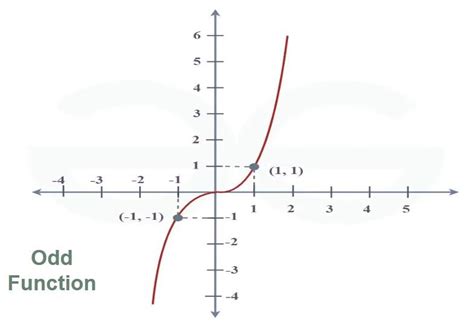
A function is "odd" when: −f(x) = f(−x) for all x Note the minus in front of f(x): −f(x). And we get origin symmetry: This is the curve f(x) = x3−x They got called "odd" because the functions x, x3, x5, x7, etc behave like that, but there are other functions . Tingnan ang higit paAdding: 1. The sum of two even functions is even 2. The sum of two odd functions is odd 3. The sum of an even and odd function is . Tingnan ang higit pa
Don't be misled by the names "odd" and "even" . they are just names . and a function does not have to beeven or odd. In fact most functions are neither odd nor even. For . Tingnan ang higit paEven and odd functions are named based on the fact that the power function f(x) = x n is an even function, if n is even, and f(x) is an odd function if n is odd. Let us explore other even and odd functions and .In mathematics, an even function is a real function such that for every in its domain. Similarly, an odd function is a function such that for every in its domain. They are named for the parity of the powers of the power functions which satisfy each condition: the function is even if n is an even integer, and it is odd if n is an odd integer.A function can be defined as even, odd or neither in different ways, either algebraically or graphically. A function is called an even function if its graph is unchanged under reflection in the y-axis.How to Determine if a Function is Even, Odd or Neither. I have prepared eight (8) worked examples to illustrate the procedure or steps on how to figure out if a given function is even, odd, or neither. The math .define even and odd functionWhen we are given the equation of a function f(x), we can check whether the function is even, odd, or neither by evaluating f(-x). If we get an expression that is equivalent to .Even and odd are terms used to describe the symmetry of a function. An even function is symmetric about the y-axis of the coordinate plane while an odd function is symmetric about the origin. Most functions are .
Even and odd functions are functions that satisfy certain properties. This is a powerful concept; identifying even and odd functions can make some seemingly tough integration .About. Transcript. Even functions are symmetrical about the y-axis: f (x)=f (-x). Odd functions are symmetrical about the x- and y-axis: f (x)=-f (-x). Let's use these .
Even and odd functions: Graphs (video) | Khan Academy. Google Classroom. Microsoft Teams. About. Transcript. Sal picks the function that is odd among three functions given .
define even and odd function odd or even functionAlthough even roots of negative numbers cannot be solved with just real numbers, odd roots are possible. For example: (-3) (-3) (-3)=cbrt (-27) Even though you are multiplying a negative number, it is possible to obtain a negative answer because you are multiplying it with itself an odd number of times. Let's walk through it a little more slowly:
Even and Odd Function Graphs. Consider, now, the graphs of the functions presented in the previous section: Example 1. f ( x) = x 2. Figure 1. Graph of x squared. This graph has a reflectional .

Even and odd functions are types of functions. A function f is even if f (-x) = f (x), for all x in the domain of f. A function f is an odd function if f (-x) = -f (x) for all x in the domain of f, i.e. Even function: f (-x) = f (x) Odd function: f (-x) = -f (x) In this article, we will discuss even and odd functions, even and odd function .
So, a function can never be symmetrical around the x-axis. Just remember: symmetry around x-axis ≠ function. To answer your second question, "even" and "odd" functions are named for the exponent in this power function: f (x) = xⁿ. - if n is an even integer, then f (x) is an "even" function. - if n is an odd integer, then f (x) is an "odd .
Watch this video to learn how to identify even and odd functions from tables of values. You will see examples of functions that are symmetric about the y-axis or the origin, and how to use the algebraic test f(-x) = f(x) or f(-x) = -f(x). Khan Academy offers free, world-class education for anyone, anywhere.odd or even functionEven and odd functions fulfill a series of properties, which are: Every real function is equal to the sum of an even function and an odd function. The constant function 0 is the only one that is both even and odd at the same time. The product of two even functions is an even function. The product of two odd functions is an even function.Even and odd functions: Graphs and tables. This table defines function f : According to the table, is f even, odd, or neither? Learn for free about math, art, computer programming, economics, physics, chemistry, biology, medicine, finance, history, and more. Khan Academy is a nonprofit with the mission of providing a free, world-class education .An even function is one whose graph exhibits symmetry about the y -axis; an odd function is one whose graph exhibits symmetry about the origin. Which is a fancy way of saying that, if you split the graphs down the middle at the y -axis, an even function's halves will mirror each other exactly, while an odd function's halves with be upside-down .Functions can be symmetrical about the y-axis, which means that if we reflect their graph about the y-axis we will get the same graph. There are other functions that we can reflect about both the x- and y-axis and get the same graph. These are two types of symmetry we call even and odd functions. Created by Sal Khan. Questions.
In the below program – we are creating a function named " CheckEvenOdd () ", it accepts a number and returns "EVEN" if the number is EVEN or returns "ODD" if the number is ODD.
Check Even or Odd Number using the modulo operator in Python. In this method, we use the modulo operator (%) to check if the number is even or odd in Python. The Modulo operator returns the remainder when divided by any number so, we will evaluate the x%2, and if the result is 0 a number is even otherwise it is an odd number. .Algebraically, without looking at a graph, we can determine whether the function is even or odd by finding the formula for the reflections. f(−x) = −f(x) for all x. . In calculus an odd function is defined as, −f(x) = .Even and Odd Extensions. Suppose that a function f (x) is piecewise continuous and defined on the interval [0, π]. To find its Fourier series, we first extend this function to the interval [−π, π]. This can be done in two ways: We can construct the even extension of f (x) : or the odd extension of f (x) : For the even function, the Fourier .W3Schools offers free online tutorials, references and exercises in all the major languages of the web. Covering popular subjects like HTML, CSS, JavaScript, Python, SQL, Java, and many, many more.Even and Odd Functions. Even and odd functions are functions that satisfy certain properties. This is a powerful concept; identifying even and odd functions can make some seemingly tough integration problems trivial. Even functions are functions that satisfy f (x) = f (-x) f (x) = f (−x) for all x x. Even functions are symmetric about the .Term. Definition. Even Function. An even function is a function with a graph that is symmetric with respect to the -axis and has the property that . Odd Function. An odd function is a function with the property that . Odd functions have rotational symmetry about the origin.
It is important to remember that a functiondoesnot have to beeven or odd. Most functions are neither even nor odd. To determine whether the function y = 3 (x + 2) 2 + 4 is even or odd, apply the test for both types. Apply the test for an even function: f (− x) = 3 (− x + 2) 2 + 4 = 3 (x − 2) 2 + 4 ≠ f (x). The function is not an even .
define even and odd function|odd or even function
PH0 · odd or even function
PH1 · even function graph
PH2 · Iba pa